Understanding why keep change flip works will make your student more successful in high school math. In about the 5th grade, your student may have heard the phrase "Keep Change Flip" when learning how to divide fractions. It is a mnemonic used in many 5th grade math classes to represent the steps to divide fractions. This worked great in middle school math and it got the student the right answer when used correctly.
In high school, students need to understand why keep change flip works.
The following is a review of how keep change flip works.
 | We want to divide fraction 1/5 by another fraction 2/3. |
 | Remember the phrase keep change flip. |
 | 1) Keep the 1st fraction the same. 2) Change to operator from division to multiplication. 3) "Flip" the 2nd fraction. For this fraction, the numerator becomes the denominator and the denominator becomes the numerator. |
 | Multiply the fractions like you normally do. |
 | Simplify to the final answer. |
Now lets look at why keep change flip works.
 | Again we want to divide the fraction 1/5 by the fraction 2/3. |
 | Rewrite the problem as shown here. |
 | Determine the reciprocal of the fraction in the denominator. |
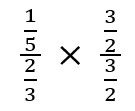 | Multiply the numerator and the denominator from the original problem by the reciprocal of the denominator as determined from the previous step. Note: This does not change the value of the original problem because 3/2 over 3/2 is equal to 1. |
 | Details of multiplying the fractions. |
 | Further detail of multiplying the fractions. |
 | Still further detail of multiplying the fractions. |
 | Final answer. |
Your student will need guided practice to master this concept.
Most students have gaps in their math knowledge. There are all sorts of reasons for this. To eliminate these gaps, it can be so helpful to work with an experienced professional tutor to find these gaps and address them (in the right way). This includes patience, kindness and building/maintaining confidence while gently, strategically and consistently bringing the student forward. Each student is different. The tutor will need to ask the right questions, then carefully listen, watch and observe how the student works out the problems to find gaps that may not be revealed in a math assessment. Further, having the student read the word problems out loud will help to uncover words that are unfamiliar to the student. These words need to be addressed by the tutor. In this way, the math tutor is teaching reading and vocabulary (to boost the student's understanding) as well as teaching math. This vocabulary will include math vocabulary as well as other general vocabulary.
Click here if you would like to work with a Pre-Algebra tutor online.
Click on the image below for a video version of this blog.
Author: Sigrid Kimbrough, ThriveMathTutoring.com
Comments